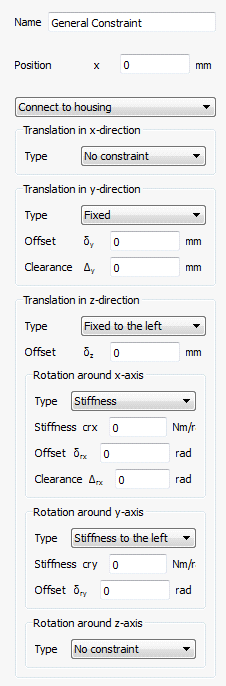
 Die "Allgemeine Randbedingung" erlaubt die Definition von Bedingungen zwischen einer Welle und dem Gehäuse oder zwischen zwei Wellen für alle sechs Freiheitsgrade unabhängig voneinander.
Die "Allgemeine Randbedingung" erlaubt die Definition von Bedingungen zwischen einer Welle und dem Gehäuse oder zwischen zwei Wellen für alle sechs Freiheitsgrade unabhängig voneinander.
Zunächst kann ausgewählt werden, mit welchem Element die Welle verbunden ist. Das kann das Gehäuse oder eine zweite Welle sein.
Für jeden Freiheitsgrad kann dann ein Typ von Zwangsbedingung definiert werden:
•Keine Bedingung: Es wird keine Bedingung in der Richtung definiert.
•Fest: Der Freiheitsgrad zwischen beiden Elementen ist sowohl in positiver als auch in negativer Richtung gekoppelt. Optional kann ein Versatz oder ein Spiel definiert werden. Ein positiver Wert für den Versatz resultiert in einer Bewegung der aktuellen Welle in diese Richtung bzw. in einer Kraft auf die ausgewählte Welle in dieser Richtung. Das Spiel ist entweder Null oder ein positiver Wert, er darf nicht negativ sein. Das Spiel ist als Abstand zwischen den beiden Endwerten definiert.
•Fest nach links (oder rechts): Die Auswahl "Fest nach links" bedeutet, dass die ausgewählte Welle nur in negativer Richtung (links auf einer horizontalen Achse) belastet wird. "Fest nach rechts" bedeutet, dass die Beschränkung nur in positiver Richtung gilt. Für die unidirektionale Beschränkung kann ein Versatz definiert werden.
•Steifigkeit: Die "Steifigkeit" wirkt wie eine Feder. Es kann ein Versatz und ein Spiel definiert werden. Versatz und Spiel werden wie oben für "Fest" beschrieben definiert.
•Steifigkeit nach links (oder rechts): Wie bei der Fest-Bedingung kann auch die Steifigkeit nur in eine Richtung definiert werden. Es können die Steifigkeit und ein Versatz definiert werden.
Mit der  -Schaltfläche kann der axiale Versatz in x-Richtung basierend auf einer vorgegebenen Vorspannung berechnet werden. Der Versatz wird so lange variiert, bis die Axialkraft auf das Lager gleich der Vorspannung ist. Das Vorzeichen des Wertes der Vorspannung ist wichtig. Die Berechnung funktioniert nur, wenn die Welle vollständig definiert ist und basiert auf einer iterativen Lösung des gesamten Wellensystems.
-Schaltfläche kann der axiale Versatz in x-Richtung basierend auf einer vorgegebenen Vorspannung berechnet werden. Der Versatz wird so lange variiert, bis die Axialkraft auf das Lager gleich der Vorspannung ist. Das Vorzeichen des Wertes der Vorspannung ist wichtig. Die Berechnung funktioniert nur, wenn die Welle vollständig definiert ist und basiert auf einer iterativen Lösung des gesamten Wellensystems.